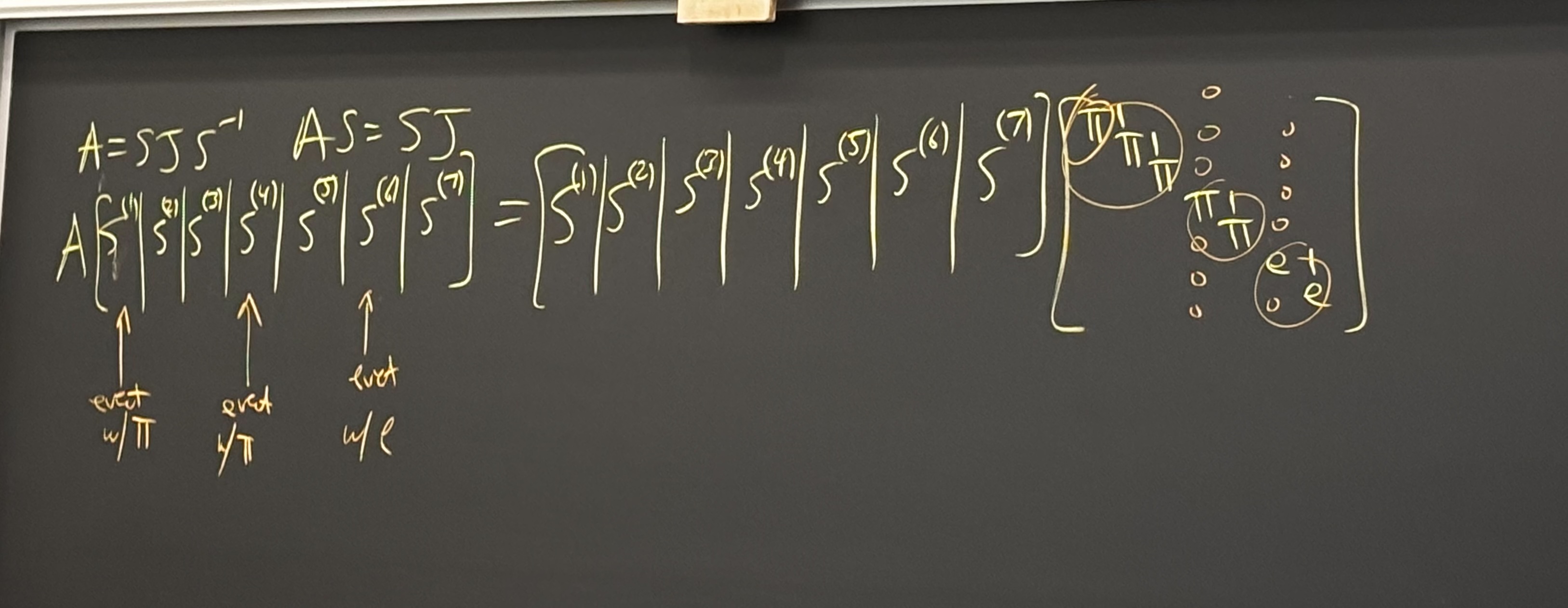Lecture 12
[[lecture-data]]
Exam in about 2 weeks - choose the "least bad" date.
2024-09-23
Readings
- a
3. Chapter 3
Jordan's theorem
Recall the statement of Jordan's Theorem from last Lecture Lecture 11. Today we do the proof: uniqueness (+existence maybe later or just reading)
For each
for
(see Jordan's Theorem)
When we say Jordan block we mean having eigenvalues along the diagonal and all
Consider a special case,
Note that
(this is for when the all eigenvalues are
Consider a sequence of non-increasing natural numbers. This can be considered a partition of their sum.
We can draw a Ferrer's Diagram of this sequence. And we can take the "transpose" or look at the number of blocks on the left side. And this gives another partition of the sum.
The dual sequence is "counting the blocks" on the left side.
So order the
If
ie, we can deduce the block structure from
More generally, suppose
What if we take
So we have that
And the blocks $$\begin{bmatrix}
J_{n_{q}}(\neq 0)^\ell & & \
& J_{n_{q+1}}(\neq 0)^\ell & \
& & \ddots
\end{bmatrix}$$ are invertible! Since we know the eigenvalues are not zero. As we increase
- we can observe the difference in the rank of the matrix for the successive powers of
, and that will tell us the sizes of the blocks for the first eigenvalue - We can then repeat this process with each eigenvalue to recover the block structure associated with each eigenvalue of
, and thus the form of !
If
For
In particular, for any eigenvalue, the geometric multiplicity has the property that
So what is the geometric multiplicity of
Suppose
We know that
By the theorem above, this means that we get the same Jordan canonical form for each of them, meaning they are similar to the same matrix. And since similarity is an equivalence relation, they are similar to each other as well!