[[lecture-data]]

2025-02-18

Readings

• a

n. Subject

Invariant functions on sets
Zaheer et al 2017
Goals:

1. Define a class of functions that can deal with sets/multisets as inputs
2. Translate this class of functions into an efficient neural network
3. Show that it works well (state-of-the-art) for several real-world applications

Sets/multisets $\{x_1,\dots ,x_n\}=\{x_{\sigma (1)},\dots ,x_{\sigma (n)}\}$ for all permutations $\sigma :[n]\to [n]$
+++ see notes
We can think of these as ${\mathbb{R}}^n/S_n$, or unordered tuples from the reals

example
$(1,1,2)=(1,2,1)\ne (1,2)$

Motivation

• sometimes the order is not important for the "downstream task"
• Applications in the paper
  • learning to estimate pop stats (mean, variance)
  • learning to sum digits from images
  • point cloud classification
  • outlier detection
  • predicting a set of tags (for text)

prior implementations of invariant functions on these sets
$f:{\mathbb{R}}^n\to \mathbb{R},f(x_1,\dots ,x_n)=f(x_{\sigma (1)}\dots ,x_{\sigma (n)})$

Invariant polynomials

• $f$ is poly that can be written as combo of elementary symmetric polynomials

$e_1(x_1,\dots ,x_n)=\sum _{i=1}^n{x}_i,e_2=\sum _{1\le i\le j\le n}{x}_i{x}_j,\dots ,e_n=x_1{x}_2\dots x_n,e_{n+1}=0$
Equivalently $e_1=\sum _i{x}_i,e_2=\sum _i{x}_i^2,e_3=\sum _i{x}_i^3,\dots e_n=\sum _i{x}_i^n$ is also a basis/generator for my symmetric polynomials
+++++ see notes

This requires $n$ polynomials of degree $n$.

Another way to describe them

Canonicalization

Given $(x_1,\dots ,x_n)$, find $\sigma \in S_n$ that sorts the entries such that
$x_{\sigma (1)}\le x_{\sigma (2)}\le \cdots \le x_{\sigma (n)}$
A function $h$ is invariant then $⟺$ $h$ is a function of the sorted entries

choose a "representative" or "template" of my tuple

Deep Sets Paper

Input $X=\{x_1,\dots ,x_m\},x_i\in X$ where $X$ is countable. Consider space of functions $f:2^X\to \mathbb{R}$
$f$ is permutation invariant if and only if $f$ can be decomposed as

for suitable $\varphi :X\to \mathbb{R}$ and $\rho :\mathbb{R}\to \mathbb{R}$

• sum does not need to be a sum. Just needs to be a permutation invariant function applied to each element in the set

(can think of this as a layer in a neural network)

Wait whoa

• Can write an invariant function as a sum of just one feature per element

Previous polynomial representation, we needed $n$ features per element.

• will see in proof that perhaps we can get simpler representations by using a higher dimensional latent space ($\varphi :X\to {\mathbb{R}}^k$)

Note

in 2nd lecture

• if $f(x)$ and $G$ is finite then $f(x)=\frac{1}{|G|}=\sum _{g\in G}\tilde{f}(g\circ x)$ (group averaging)

Here, $G=S_m$, permutations in $M$ objects. So $|G|=M!$ which is a huge set

But Deep Seets tells us that we only need to sum over $M$ objects instead of $M!$

Proof (sketch)
$(⟹)$ Suppose we have a function $f(x)$ such that

$f$ is permutation invariant to permutation $\pi$:

$(⟸)$ (not the cleanest version, but first paper showing this)

1. use $\varphi$ to encode each possible input into a real number
   • injective over the whole set of sets
2. learn $\rho :\mathbb{R}\to \mathbb{R}$ that executes that function on the set

Since $X$ is countable, there exists a bijection $c:X\to \mathbb{N}$. We can encode each subset of $X$ (ie each element of $2^X$)

Let $Y\subset X$. We can encode $Y$ as a binary sequence $0.a_1{a}_2{a}_3\dots a_j\dots$
such that $a_j=1⟺x_i\in Y$

• this gives us a real number per orbit and then learning an invariant function is the same as learning the function in each orbit representative

There are also better theoretical proofs of the same thing Tabaghi and Wang 2024
$f:{\mathbb{R}}^{k\times n}\to {\mathbb{R}}^s$

• sets of $n$ elements in ${\mathbb{R}}^k$

If this function is $S_n$ invariant (permutation invariant to the elements in the set), then there exists some
$\varphi :{\mathbb{R}}^k\to {\mathbb{R}}^{\ell }$ and $\rho :{\mathbb{R}}^{\ell }\to {\mathbb{R}}^s$ such that

and $\ell$ can be chosen such that $\ell \le 2kn$

architecture (++++++see notes)

point clouds

invariant functions on point clouds

motivation:

• emulation of cosmological simulations
• galaxy properties preditions from dark matter using only simultations
  "regression" framework for these types of movements
  ++++ see notes

$n$ points in $d$ dimensions

• invariant to translations
• rotations
• reflections

$f:{\mathbb{R}}^{d\times n}\to \mathbb{R},E(d)$ invariant and $v\to f(v)$ permutation invariant

translations

• center point cloud (translation invariance w sorting getting permutation invariance - choosing a representative from our orbit)

permutations
Want $O(d)$ and $S_n$

• $f:v\to \mathbb{R}$ is $O(d)$ invariant $⟺$ $f(v)=\tilde{f}(V^{T}V)$
• where $V^{T}V$ is gram matrix
• $f(v\pi )=f(v)⟹\tilde{f}({\pi }^T{V}^{T}V\pi )=\tilde{f}(V^{T}V)$
  $\tilde{f}$ invariant by permutations acting by conjugations
• symmetry of graphs that we saw in the first class
  • Graph neural networks (cover GNNs in next lectures)

want functions that are invariant to permutations of rows and columns

Why invariant theory?

1. construct the graph with $O(n^2)$ complexity, we'll be able to learn invariant functions with $O(nd)$ complexity
2. ++++ see notes
3. Galois theory - interesting mathematical properties

Galois Theory (setup)
$S_n$ is acting by conjugation (permuting rows and columns)

• always sending diag to diag and off-diag to off-diag
• (permuting rows and columns at the same time)

the $S_n$ above is a subgroup of$S_n\times S_{(\genfrac{}{}{0ex}{}{n}{2})}$ (which are off-diag to off-diag and diag to diag independently)

++++see notes
$f$ is $S_n$ invariant then if $f$ is $S_n\times S_{(\genfrac{}{}{0ex}{}{n}{{}_2})}$ invariant also
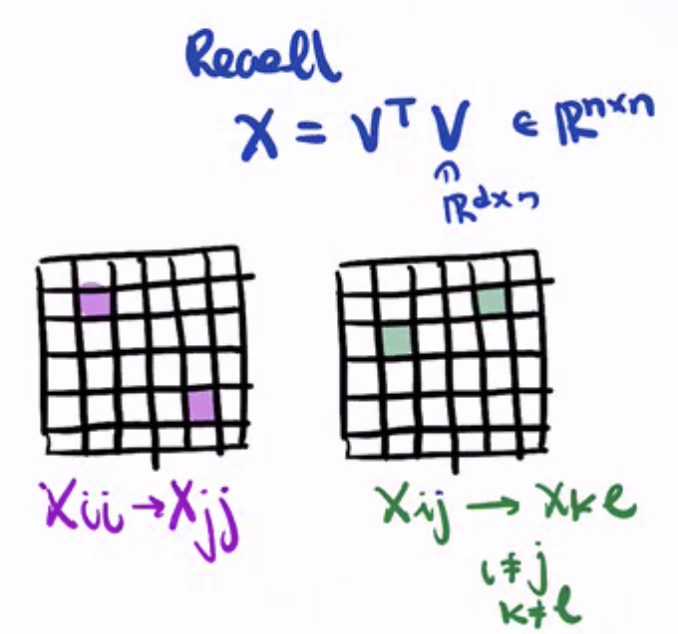
$f^d,f^o$ characterize ++++ notes

Galois theory approach

• idea: if we construct a set of invariants that are only fixed by the desired group (ie no other bigger group fixes all the invariants) then those invariants generate the field of invariant functions
• (fundamental theorem rephrased)
  Rosenlicht (1956) the orbits that the field generators fail to uniquely identiyfy (bad) has to satisfy that a finite set of equations (bad set is measure zero)

$Id\subseteq S_n\subseteq S_n\times S_{(\genfrac{}{}{0ex}{}{n}{2})}$

• field extension $\mathbb{R}(f^{\ast }=\sum _{i\ne j}{x}_{ii}{x}_{ij})$ "ties up" the permutation of diagonals and off diagonals
  • constrains the consistency of the permutation between diagonals and off diagonals
  • this generates the field of invariant functions
• can construct a polynomial that satisfies this property

++see notes

$\mathbb{R}(f^d,f^o)=\frac{\text{polynomials generated by }(f^d,f^o)}{\text{polynomials generated by }(f^d,f^o)}$
$f^d=\{\sum x_{ii},\sum x_{ii}^2,\dots \}$
$f^o=\{\sum _{i\ne j}{x}_{ij},\sum _{i\ne j}{x}_{ij}^2,\dots \}$

that is the field generated by $f^d$ and $f^o$ and the sets are field generators for the space.
And note that $\mathbb{R}(f^d,f^o,f^{\ast })$ is algebraically independent from $\mathbb{R}(f^d,f^o)$.

• separating orbits under group actions is considered

(galois theory is not a necessary argument, uses easier argument - construct set of invariants that are only fixed by desired group, then can separate orbits almost everywhere)

using Deep Sets
universally approximate invariant functions on symmetric function sets outside an invariant, closed, zero-measure "bad set" where orbits are not separable

From $O(n^2)$ to $O(nd)$ invariant features
$V=[v_1\dots v_n]\in {\mathbb{R}}^{d\times n}$

• consider $C(V)\in {\mathbb{R}}^{d\times k}$ "centers" that is $O(d)$ and S_n invariant
  • ex $k$-means centroids ordered by 2norm

$VC=[]$

Invariant machine learning model with $O(nd)$ features :
$V\to h(\text{deepset}(C^{T}V),C^{T}C)$ and this is $S_n$ invariant

Theorem (Huang Blum-Smith 2024 etc)

• the machine learning model above can universally approximate invariant functions on symmetric function sets outside an invariant, closed, zero-measure "bad set" where orbits are not separable