2025-04-02 lecture 17
[[lecture-data]]
3. Graphon Signal Processing
Does the GFT converge to the WFT?
And why do we care?
high variance of small samples might obscure important information in a signal's GFT, like the correlation with respect to the graph structure. Since the limiting graphon has no noise, it can reveal the "real"/intrinsic structure of the signal.
convergence of signals in the Fourier domain
Recall
- convergent graph signals
and - eigenvalues of the induced graphon converge pointwise to the eigenvalues of the limit ie
for all
first approach: using convergence of signal and eigenvalues
Recall that
In order to have convergence of the graph fourier transform to the graphon fourier transform, we need {1||convergence of the graph (filter) eigenvectors||convergence} to the {1||graphon (filter) eigenfunctions||to}
Let
Where
Call the first interior min

If
Let
This is good because from lecture 15, we know that if
Does this mean everything is OK?
- No! The denominator might vanish as
since we have from the second part of the spectral theorem for self-adjoint compact operators on Hilbert spaces - even though we look at
and converge to different values (and therefore ), it still might not work.
- even though we look at
- Even if we have eigenvalue convergence, this convergence is not necessarily uniform. (recall the difference between convergence and uniform convergence) because the graphon eigenvalues accumulate at 0.
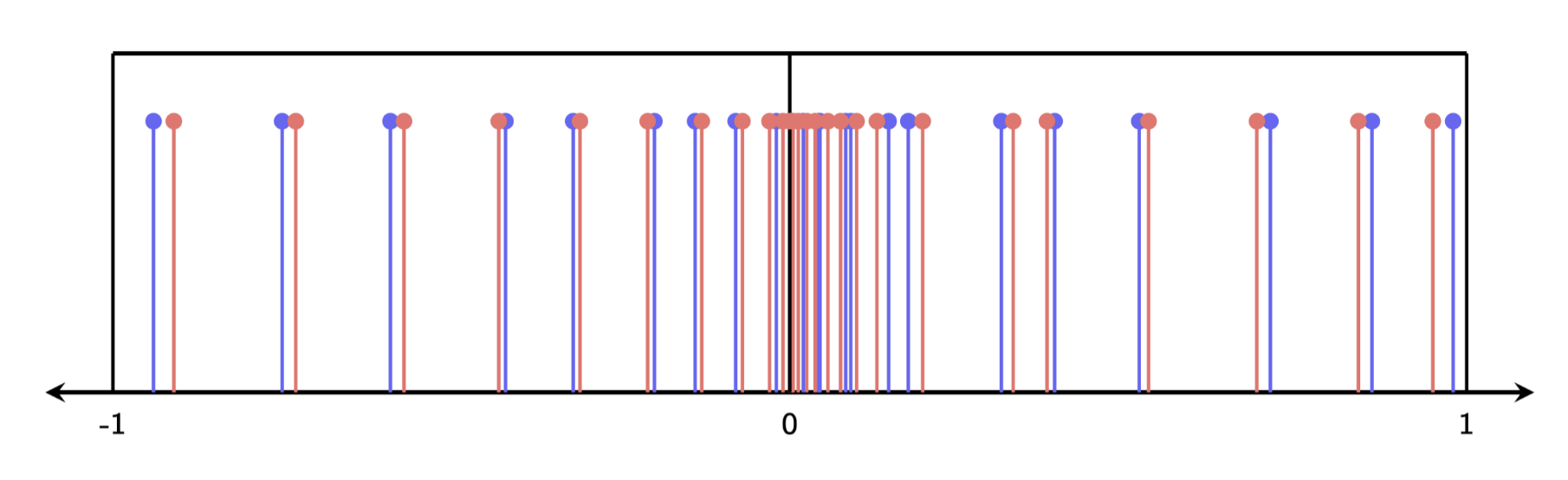
Convergence holds in the sense that for all
However,
- this is a limitation of graphons
- for dense graphs this is useful
- bounded spectrum
- sparser graphs do not have convergence of spectra, so they are harder to deal with as well
Though the eigenvalues converge, they do not converge uniformly since their accumulation is at 0.
So conjecture 1 is wrong, but in the right direction
approach 2:
A graphon signal
see bandlimited graphon signal
"Limiting" the energy to a middle "band" of frequencies about
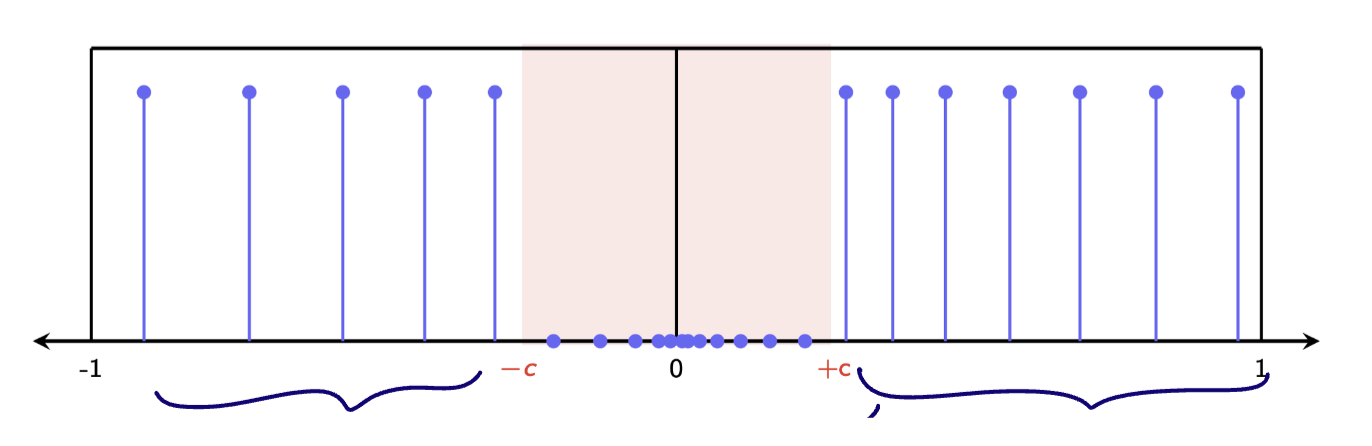
Let
Let
Let
By convergence of
And for
And from
Thus, for any
And for
Where
see bandlimited convergent graph signals converge in the fourier domain
Graphon Convolutions
WFT is the {1||algebraic equivalent} of GFT; graphon filters have the same {1||algebraic structure} of graph filters. These are the same {2||shift-and-sum} operations, but now the {2||shift} is the graphon shift
Like graph convolutions, graphon convolutions also have a spectral representation (see spectral representation of graphon convolutions)
Given a graphon convolution with input graphon signal
Where
This is a simple result following the diagonalization of
Some interesting takeaways (analogues of the graph convolution)
- Like the WFT, the spectral response of a graphon convolution is discrete
- the spectral response of the graphon convolution is also pointwise in that the
th spectral component of the output only depends on and - ie
depends only on and
- ie
- The spectral response of
given by is independent of the underlying (like the spectral response of was independent of the graph) - ie, the spectral response can be written as a polynomial function. The eigenvalues of the graphon determine where we evaluate this function. (samples of function that is eigenvalues/spectrum)
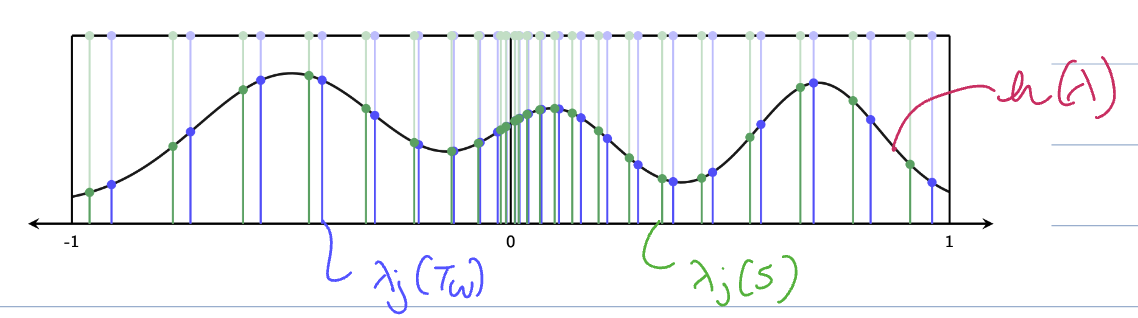
Given the same (fixed) coefficients
- this is the same as the spectral representation of graphon convolutions/function for the same coefficients.
- The only difference is where the function is evaluated.
- For a graphon, we evaluate it at the graphon shift operator eigenvalues
for graphon signal - For a graph, this is the graph shift operator eigenvalues
for the graph signal
- For a graphon, we evaluate it at the graphon shift operator eigenvalues
Why do we care?
Given a convergent graph sequence
And if we fix coefficients
Given
in the sense that
the graph convolution converges to the graphon convolution (with the same filter coefficients) in the spectral domain.
This says
- Convergence of the graph convolution to the graphon convolution in the spectral domain (first line)
- Convergence of the spectral response of the graphon convolution on the induced graphon converges pointwise to the spectral response of the limiting graphon convolution (second line)
And this holds for all eigenvalue indices
Spectral convergence is not enough to do what we want. Graph convolutions operate in the node domain.
Review
We'd like to use the Davis-Kahan Theorem to bound the distance between the eigenfunctions of the induced graphon shift operator and the limiting graphon shift operator to show convergence in the Fourier domain. Why does this fail? (2 reasons)
-?-
- The denominator of the bound might vanish because
as (the distances are getting smaller and smaller) - The eigenvalues only accumulate at 0. This means we may have non-uniform convergence in the eigenvalues
{1||bandlimited||condition} convergent graph signals converge {2||in the fourier domain.||result (how/where)}
Created 2025-04-02 ֍ Last Modified 2025-08-18