2025-03-26 lecture 15
[[lecture-data]]
2. [[GNN Analyses]]
Last time, we left off defining a metric for graphs with potentially different node counts.
Let
We want to use the induced graphons (recall we do this by dividing the interval
However, the cut norm does not take into account {ass||permutations of the intervals
Thus, for two arbitrary graphs, we can define the cut distance:
Let
Where
see [[cut distance]]
We can show equivalence of right- and left- cut [[homomorphism density]] convergence with the [[cut distance]] for dense graphs.
Sequences of graphs
Where
see [[graph sequence converges if and only if the induced graphon sequence converges]]
In fact, to show that left and right convergence with the cut metric/[[cut norm]] as above.
Proofs are in the book Large networks and convergent graph sequences by Lavàsz (online). For the equivalence in [[homomorphism density]], see section counting and inverse counting lemmas.
This answers the question that we had last time
What happens when the graph grows?
- Can we measure how “close” two large graphs are? ie, can we define a metric for two large graphs?
The limiting object of a [[convergent graph sequence]] is a [[graphon]]. We use the (left) [[homomorphism density]] to show this convergence.
The induced graphons.
Now, we address
2. Can we prove the GNN is continuous WRT to this metric?
Relationship between the graphons
(and [[graphon distances]] which have codomain
Let
Trivially:
Easy to see from definition of [[cut norm]] where we are essentially computing the
convergence in implies cut norm convergence
Let
And convergence
Easy to see (1) from the definition of the cut norm:
This is computing the L-1 norm restricted to a subset of the nodes, so
. (2) and (3) are a common result from functional analysis, and (4) is because of the selected codomain for
. Convergence in the [[cut norm]] follows immediately from this hierarchy.
see [[convergence in L-p implies convergence in cut norm]]
In the other direction:
Let
ie, [[cut norm]] convergence implies convergence in
see [[Convergence in the cut norm implies convergence in L2]]
We first show inequality (2). Using the definition of the [[cut norm]], we have
Since we are taking the supremum, it is equivalent to taking the supremum over all
To get
- or equivalently that
We can then see that the definition becomes the absolute value of the inner product of twofunctions.
Note that
- we omit the denominator in our usual definition of the [[operator norm]] since
is bounded by and and - We can rewrite this using
to match in the definition of the norm since we are taking the supremum - For more about
spaces see wikipedia (hand wavy/cursory for this class on functional analysis details)
We can then rewrite this as
Where we get
- Note that this is a loose bound!
And this gives us the desired result for (2).
Proving (1) is more involved and uses more functional analysis.
Use the Riesz-Thorin interpolation theorem for complex
Where
and - with
and and .
Define [[operator norm]]$$\lvert \lvert W \rvert \rvert_{\square, \mathbb{C}} = \sup_{\begin{aligned}
f,g:[0,1] &\to \mathbb{C} \\lvert \lvert f \rvert \rvert_{\infty}, \lvert \lvert g \rvert \rvert_{\infty} &≤1 \end{aligned}} \left\lvert \int {0}^1 \int^1 W(u,v) f(u) g(v) , du , dv \right\rvert $$
So for complex functions, we can see that
We then have
Since
convergence in the 2 norm
idea/preview
If we have a sequence of convergent graphs that converges to a [[graphon]], then the [[graph shift operator]] (typically
see [[graph shift operators converge to graphon shift operators]]
- We defined [[convergent graph sequence]] converging to [[graphon]]
- If two graphs belong to the same sequence, we know they are similar using the [[homomorphism density]]
- Defined a metric with the cut metric to compute distances between graphs
- If we have convergence in some
spaces, we also have convergence in the [[cut norm]] and vice versa. - We can look at graphons as operators
can we use graphons to sample subgraphs?
Recall the question we had
What if the graph is too large and I don’t have enough resources to train on it? (recall GNN forward pass is
we can think of graphons as generative models as well
Graphon as a limiting object for some sequence of graphs

Graphon as generating object for finite graphs

options for sampling nodes and edges from graphons
- [[template graph]]
see [[ways to sample graphs from graphons]]
A template graph
So that
The [[adjacency matrix]] is then given as
Where
This is a complete, weighted graph with edge weights coming from the [[graphon]] evaluated at each node pair
This is the simplest way to sample a graph. We can think of it as the graph sampling counterpart to inducing a graphon.
see [[template graph]]
Weighted graphs are a way to sample a graph from a graphon. Each node
The edges are then defined in the same way as a [[template graph]]
see [[weighted graph (sample)]]
Fully random graphs are a way to sample a graph from a graphon. Like a [[weighted graph (sample)]], the nodes are sampled uniformly from the unit interval (
The edges are sampled as
So the resulting graph is undirected and unweighted .
see [[fully random graph]]
Generally we are interested in the fully random graphs.
- [?] could we sample the nodes randomly, then sample the edge weights from the 2D interval?
All of the graphs above converge to
Template graphs: trivial
Let
Trivial
- The definition of template graphs is fully deterministic, so there is no randomness here. Since this is the reverse idea of thinking of graphons as graphs with uncountable number of nodes, it is easy to see that the induced graphons
converge to in an way and [[convergence in L-p implies convergence in cut norm]]
see [[template graphs converge to the graphon]]
Let
Where
see [[weighted sampled graphs converge to the graphon in probability]]
random
Let
Where
see [[fully random graphs converge to the graphon in probability]]
We'll look at the proofs for these later.
If a graph is too big to train on it, we can look at the [[induced graphon]] and subsample new graphs from it to train on instead.
GNN continuity
How do we determine whether a GNN continuous with respect to the cut metric?
In order to transfer from small graphs to large graphs, we need continuity. In particular, we need Lipschitz continuity with a not-very-large constant.
Do GNNs converge?
This question has a long answer. To start to answer it, we need to introduce graphon signals and graphon signal processing.
- These are extensions of [[Graph Signals and Graph Signal Processing]]
- generalize up from graphs to graphons
- graph convolution to [[graphon convolution]]
- intuition behind why GNNs generalize well with scale
- then look at bounds
- finite sampling bounds
- minimum sample sizes
- error bounds
we focus a lot on information processing pipelines and GNNs, but there are also many other applications for graphons. Many people are interested in graphon estimation / the underlying distribution for some graphs.
A graphon signal is defined as a function
contrast this with [[graph signals]], which we defined as
We focus on signals in
see [[graphon signal]]
Like a [[graphon]], a [[graphon signal]] is the limit of a [[convergent sequence of graph signals]]. Like when defining our [[cut distance]] for differently sized graphs, the [[graph signals]] may have different sizes since the dimension changes with the number of nodes
Let
Where

Both representations of 3-node graphs ([[induced graphon]] above and induced graphon signal below)
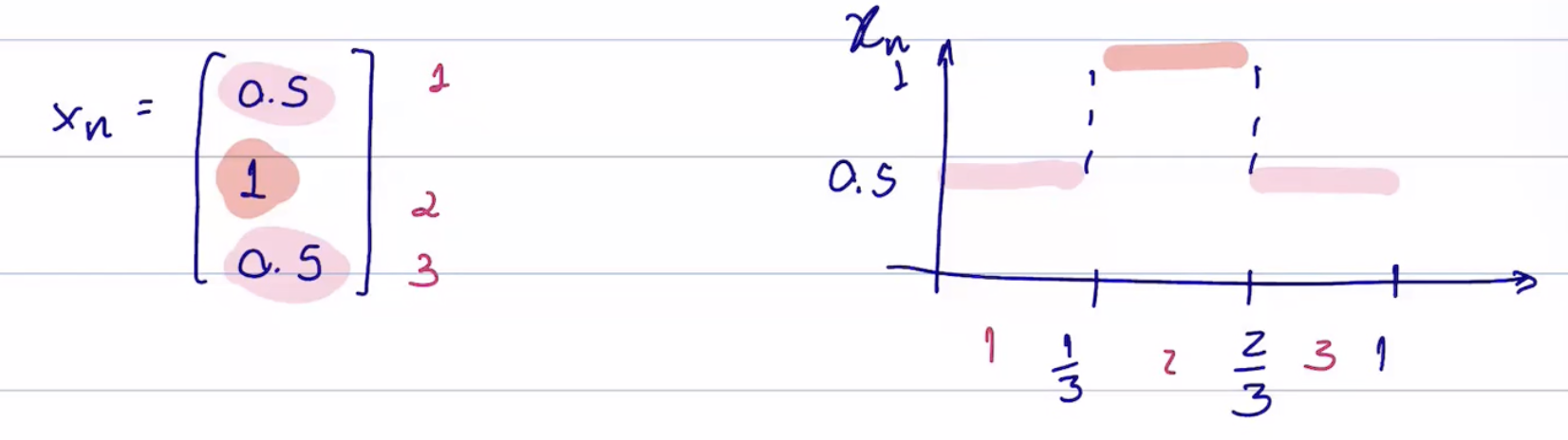
see [[induced graphon signal]]
Review
const { dateTime } = await cJS()
return function View() {
const file = dc.useCurrentFile();
return <p class="dv-modified">Created {dateTime.getCreated(file)} ֍ Last Modified {dateTime.getLastMod(file)}</p>
}