2025-03-24 graphs lecture 14

[[lecture-data]]

Summary

last time

today ([[Lecture 14.pdf]])

what if my graph grows/too large?
Graph limit: graphon

homework 2 download ➕ 2025-03-24 📅 2025-03-24 #class_notes
pick final project #class_notes 📅 2025-03-26 ✅ 2025-03-26

Homework 2 notes

val acc not stable for expressivity : normal since small val set. Loss smooth
- typical for graph-level problem
stability: 10-30% goal to see stable degrades for different models
- gnn slower than for filters
- more layers = more stable for gnn (more nonlinearities)
- discuss degradation
Last prob
- penalize vs not penalized
- plot model 2’ vs mod 2

Announcement on final project

1-2 ppl
either novel graph data/train model : 10min presentation
research paper presentation on any modern GNN/graph DS (past 5 years): 20 min presentation
- review/discussion

Limits of Graphs

Last time, we looked at different graph perturbations and how to design stable GNNs. We saw how GNNs inherit stability from their layers and that GNNs perform better than their constituent filters because of the scattering of spectral information by the nonlinear activation function.

Question

What if the graph grows?
What if the graph is too large and I don’t have enough resources to train on it? (recall GNN forward pass is $O (L K \cdot | E |)$ where $L$ is the number of layers and $K$ is the order of the filter polynomial)

To address problem 2 (what if the graph is too large?), we can subsample the graph with a random graph model. We will talk about this later.

Today, we turn to problem 1 (what if the graph grows?). To address this, we want to know

Question

Can we measure how “close” two large graphs are? ie, can we define a metric for two (large) graphs?

If we can, then we can see if a GNN is continuous. If we can prove the GNN is continuous, then we are OK (perturbations will affect the function in a predictable way). Then,

Can we prove the GNN is continuous WRT to this metric?

What does it mean for two graphs to be “close”? We’ll say this happens when they converge to a common limit.

defining a metric between graphs

What does it mean for graphs to be “close”?

From a probability POV, it makes sense to say that graphs are “close” if {sampled subgraphs have similar distributions}.
Equivalently, from a statistics POV, we say graphs are “close” if they {have similar subgraph counts (triangle counts, degrees, etc)}

To measure the subgraph counts, we can use homomorphism density. Recall from lecture 11 the definition of a graph homomorphism

Graph Homomorphism

Let $G = (V, E)$ and $F = (V^{'}, E^{'})$ . A graph homomorphism from $F$ to $G$ is a map $γ : F \to G$ such that
$(i, j) \in E^{'} ⟹ (γ (i), γ (j)) \in E^{'}$
ie, homomorphisms are adjacency-preserving maps (of $F$ ; the adjacency of $F$ must be preserved in $G$ .)

Example

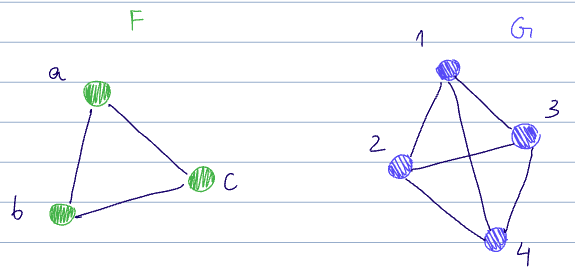
There are a few homomorphisms from $F$ to $G$ :

$(a, b, c) \mapsto (1, 2, 3)$
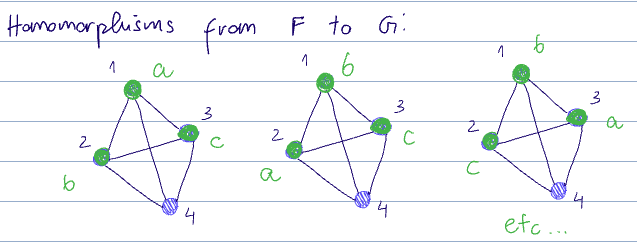
- And trivially, every permutation of $(a, b, c)$ is also a homomorphism here

There are also:

$(a, b, c) \mapsto (1, 2, 4)$
$(a, b, c) \mapsto (1, 3, 4)$
$(a, b, c) \mapsto (2, 3, 4)$
and for each of the above, each permutation of $(a, b, c)$ as well.

The homomorphism count $hom (F, G) = 24$ in this case.

Recall also the definition for the homomorphism density:

homomorphism density

Let $G = (V, E)$ and $F = (V^{'}, E^{'})$ be graphs. The homomorphism density from $F$ to $G$ , denoted $t (F, G)$ is given as
$t (F, G) = \frac{hom (F, G)}{| V |^{| V^{'} |}}$
Where $hom (F, G)$ is the the total number of homomorphisms from $F$ to $G$ .

We can think of this as the probability of sampling a version of $F$ from the graph $G$ .

Example

in the example above,

t (F, G) = \frac{24}{4^{3}} = \frac{3}{8}

This equates to the probability of sampling a triangle from $G$ when we sample 3 vertices.

The astute reader will see that we can use the homomorphism density to compare graphs from the statistics POV of sampling. To do this, we need some subgraphs that serve as references for the types of counts we want (eg. triangles).

motif

Let $F$ be a graph. $F$ is a motif if it is

undirected
unweighted
with 1 edge per node pair
not loopy (no self edges)

(see graph motif)

We can use this to create an idea of “closeness” for two graphs $G_{1}, G_{2}$ . It makes sense that $G_{1}$ and $G_{2}$ are “close” if for all motifs $F$ , we have $t (F, G_{1}) \approx t (F, G_{2})$ .

To formalize this idea into a definition, we first need to define what a convergent graph sequence is.

Convergent graph sequences and graphons

More info from Levàsz, Chayes, Borgs, Vesztergambi starting 2008-on

To begin, we need to define the “limit” of a sequence of graphs as the number of nodes $n$ grows.

We call the limit of a sequence of graphs of increasing node count a {graphon}

graphon

A graphon is a symmetric, bounded, measurable function

W : [0, 1]^{2} \to [0, 1]

ie, it is a bounded kernel (weighting function).

We can think of a graphon as a graph with an uncountable number of nodes $u \in [0, 1]$ and edges $(u, v)$ with weights $W (u, v)$ .

(see graphon)

Note

A more general definition is

W : Ω \times Ω \to [0, 1]

where $Ω$ is a sample space with some probability measure $f$ . We can always map $Ω$ onto $[0, 1]$ using a measure-preserving map (as long as the CDF of $f$ is strictly monotone), so we can use $[0, 1]^{2}$ WLOG.

Exercise

Show that if the CDF of $f$ is strictly monotone, we can map $Ω$ to the interval $[0, 1]$ with a measure-preserving map.

Note

The codomain of $W$ may be $(0, B]$ where $B \in R < + \infty$ . However, we usually have $B = 1$ since $W (u, v)$ often represents a probability.

Example

From left to right:

block model with same community sizes
different community sizes, and
$w (u, v) = \exp (\frac{(u - v)^{2}}{σ^{2}})$

If the limit of the graph sequence $G_{n}$ is a graphon, then the limit of the graph homomorphism density sequence $t (F, G_{n})$ must be the {graphon homomorphism density.}

graphon homomorphism density

The density from a graph motif $F = (V^{'}, E^{'})$ to a graphon $W$ is

\tilde{t} (F, W) = \int \int_{[0, 1]^{| V^{'} |}} \prod_{(i, j) \in E^{'}} W (u_{i}, u_{j}) \prod_{i \in V^{'}} d u_{i}

This is the generalization of the definition of the homomorphism density

If $W (u, v) < 1$ for all $u, v$ , then $t (F, W)$ can be interpreted as {the probability of sampling the motif $F$ from the graphon $W$ .}

Example

Erdos-Renyi with $p = 0.4$

(see graphon homomorphism density)

$lim_{n \to \infty} t (F, G_{n}) = \tilde{t} (F, W),, \forall, F ⟺$ ${G_{n}}_{n}$ is a convergent graph sequence with limit $W$ .

Sequence of Convergent Graphs

Let ${G_{n}}_{n}$ be a graph sequence such that $lim_{n \to \infty} t (F, G_{n})$ exists for all motifs $F$ . Then this sequence is a convergent graph sequence and its limit is given by a graphon.

(see convergent graph sequence)

This is more of a “local” idea of convergence since it checks to see if sampled subgraphs converge up to the limiting object. This is called left convergence since it deals with left homomorphism densities $t (F, G_{n})$ and $\tilde{t} (F, W)$ .
- (we count the occurrences of the motif within the graph/graphon)
This is not the only way to identify a (dense) convergent graph sequence. Another definition is based on the convergence of min-cuts or right homomorphisms $t (G_{n}, F)$ and $\tilde{t} (W, F)$ .
- This is a more “global” notion of convergence that is used sometimes by graph theorists or in physics (micro-canonical ground state energy)
Fore dense graphs, left and right convergence are equivalent (for the metric we like) without proof.
Dense graphs are ““convex””
add definition for motif #class_notes/clean ➕ 2025-03-24 📅 2025-03-24 ✅ 2025-03-24

metric on graphs

While $t (F, G)$ gives us a way to define convergent sequences of graphs, we can’t use it to measure a distance between graphs without computing $t (F, G_{1})$ and $t (F, G_{2})$ for all $F$ .

We want to use a metric that is easier to calculate. Eventually, we want a distance for arbitrary graphs $G$ and $G^{'}$ which may have different numbers of nodes. However, we begin by building our definition from the simplest case where the node counts and labels are the same.

same node count and labels

Let $G$ and $G^{'}$ be graphs with the same $n$ and the same node sets $V = V^{'}$ (ie, same node labelling).

L_{1}

norm for graphs

$L_{1}$ norm or “edit distance”

d_{1} (G, G^{'}) = | | A - A^{'} | |_{1} $ $ w h e r e $ A, A^{'} $ a r e t h e u n w e i g h t e d [[C o n c e p t W i k i / a d j a c e n c y m a t r i x ∥ a d j a c e n c y m a t r i c e s]] o f $ G, G^{'} $ r e s p e c t i v e l y .

see graph edit distance

Cut Norm

Let $B$ be a matrix. The cut norm is given as

| | B | |_{◻} = max_{S \subseteq [n], T \subseteq [n]} | \sum_{s \in S, t \in T} B_{t s} |

see cut norm

cut distance (same node count, same labels)

Let $G$ and $G^{'}$ be graphs with the same $n$ and the same node sets $V = V^{'}$ (ie, same node labelling). The cut distance is given by

d_{◻} (G, G^{'}) = | | A - A^{'} | |_{◻}

where $| | \cdot | |_{◻}$ is the cut norm.

The cut distance will be our metric of choice in most cases.

same node count, different labels

cut distance (same node count, potentially different labels)

Let $G$ and $G^{'}$ have the same number of nodes $n$ . The cut distance is given by

{\hat{δ}}_{◻} (G, G^{'}) = min_{p \in P} | | A - P^{T} A^{'} P | |_{◻}

ie, we look at all possible permutations of the nodes of $G^{'}$ WRT the node labelings of $G$ .

different node counts

Let $G_{n}$ and $G_{m}$ be graphs with $n$ and $m$ nodes respectively, where $n \neq m$ . Since these are not comparable on their own, we need to bring them into common frame of reference in order to calculate distances between them.

To do this, we can bring them into graphon space. So we need to define graphons induced by these graphs.

induced graphon

Let $G_{n}$ be a graph with $n$ nodes. The graphon induced by $G_{n}$ is

W_{n} (u, v) = \sum_{i = 1}^{n} \sum_{j = 1}^{n} A_{i j} 1 (u \in I_{i}) \cdot 1 (v \in I_{j})

where $1$ is the indicator function and $I_{k}$ is defined as

I_{k} = {\begin{cases} [\frac{k - 1}{n}, \frac{k}{n}) 1 \leq k \leq n - 1 \\ [\frac{n - 1}{n}, 1] k = n \end{cases}

see induced graphon

Example

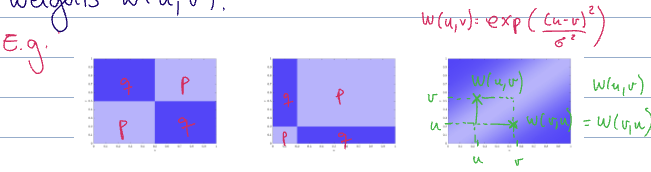
This “chops up” the axes into intervals of size $\frac{1}{n}$ and assigns values based on $A$ . We can think of this as a “heat map” of $A$ .

We can define both $G_{n}$ and $G_{m}$ as kernels on $[0, 1]^{2}$ so that they are compatible objects. This means we need a notion of the cut norm for kernels.

cut norm (kernels)

Let $W$ be a kernel in $[0, 1]^{2}$ . Its cut norm is defined as

| | W | |_{◻} = sup_{S, T \subseteq [0, 1]} | \int \int_{S \times T} W (u, v), d u, d v |

see kernel cut norm

cut metric (kernels)

For two kernels (graphons), we define the cut metric

δ_{◻} (W, W^{'}) = inf_{ϕ} | | W^{ϕ} - W^{'} | |_{◻}

Where $W^{ϕ} (u, v) = W (ϕ (u), ϕ (v))$ and $ϕ$ are measure-preserving bijections.

see kernel cut metric

#flashcards/math/dsg

Created 2025-03-24 Last Modified 2025-05-30