Last Time

Today

• G(y)ATs
• Expressivity in graph-level tasks
• Graph isomorphism problem

• This architecture is local because it is still respecting the graph sparsity pattern, and learning the "similarities" of the transformed features at each layer of the network.
• This architecture does not depend on the size of the graph, only the dimension of the features
• It can still be expensive to compute however, if the graph is dense. We need to compute $|E|$ coefficients ${\alpha }_{ij}$, which can be up to $n^2$ in complete graphs.

This additional flexibility increases the capacity of the architecture (less likely to underfit to training data), and this has ben observed empirically. But this comes at the cost of a more expensive forward pass.

This architecture is available and implemented in PyTorch Geometric

We can think of the GAT layer $(x_{\ell }{)}_i=\sigma (\sum _{j\in N(i)}{\alpha }_{ij}(x_{\ell -1}{)}_j{H}_{\ell })$ as a convolutional layer where the GSO $S$, is learned

• however, this architecture is not convolutional since $S$ is changing at each step.
• But it can be useful to see how we can write/think about it as something that looks convolutional (if you squint)

The leaky ReLU is a pointwise nonlinearity that is given as:

(see leaky ReLU)

In graph-level problems, the output does not need to be a graph signal - it could be a scalar, a class label, or some vector in ${\mathbb{R}}^d$. That is, $y\in \mathbb{R},y\in \{0,1,\dots ,C\},y\in {\mathbb{R}}^d$ are all possible.

How do we map GNN layers to such outputs?

A readout layer is an additional layer added to a GNN to achieve the desired output type/dimension for graph-level tasks or other learning tasks on graphs that require an output that is not a graph signal.

(see readout layer)

In node-level tasks (ex source localization, community detection, citation networks, etc), both the input and the output are graph signals $x\in {\mathbb{R}}^{n\times d_0},y\in {\mathbb{R}}^{n\times d_L}$. Thus, the map ${\mathrm{\Phi }}_H$ is composed strictly of GNN layers.

• Benefit: convolutional graph filters are local. This ensures a parameterization that is independent of graph size $n$

In a fully connected readout layer we define

Where

• $C\in {\mathbb{R}}^{d\times n{d}_L}$
• $\text{vec}(x_{\ell })\in {\mathbb{R}}^{n{d}_L}$
  • in general $\text{vec}(\cdot )$ vectorizes ${\mathbb{R}}^{m\times n}$ matrices into ${\mathbb{R}}^{mn}$ vectors
• $\rho$ can be the identity or some other pointwise nonlinearity (ReLU, softmax, etc)

(see fully connected readout layer)

There are some downsides of a fully connected readout layer

• The number of parameters depends on $n$ - adding $n{d}_{L}d$ learning parameters, which grows with the graph size. This is not amenable to groups of large graphs
• No longer permutation invariant because of the $\text{vec}(\cdot )$ operation

• No longer transferrable across graphs.
  • unlike in GNNs, $C$ depends on $n$. So if the number of nodes $n$ changes, we have to relearn $C$

These make this a not-so-attractive option, so we usually use an aggregation readout layer

The aggregation readout layer is a readout layer given by

where $C\in {\mathbb{R}}^{d_L\times d}$ and $\text{aggr}:{\mathbb{R}}^{n\times d}\to {\mathbb{R}}^{1\times d}$ is node-level aggregation

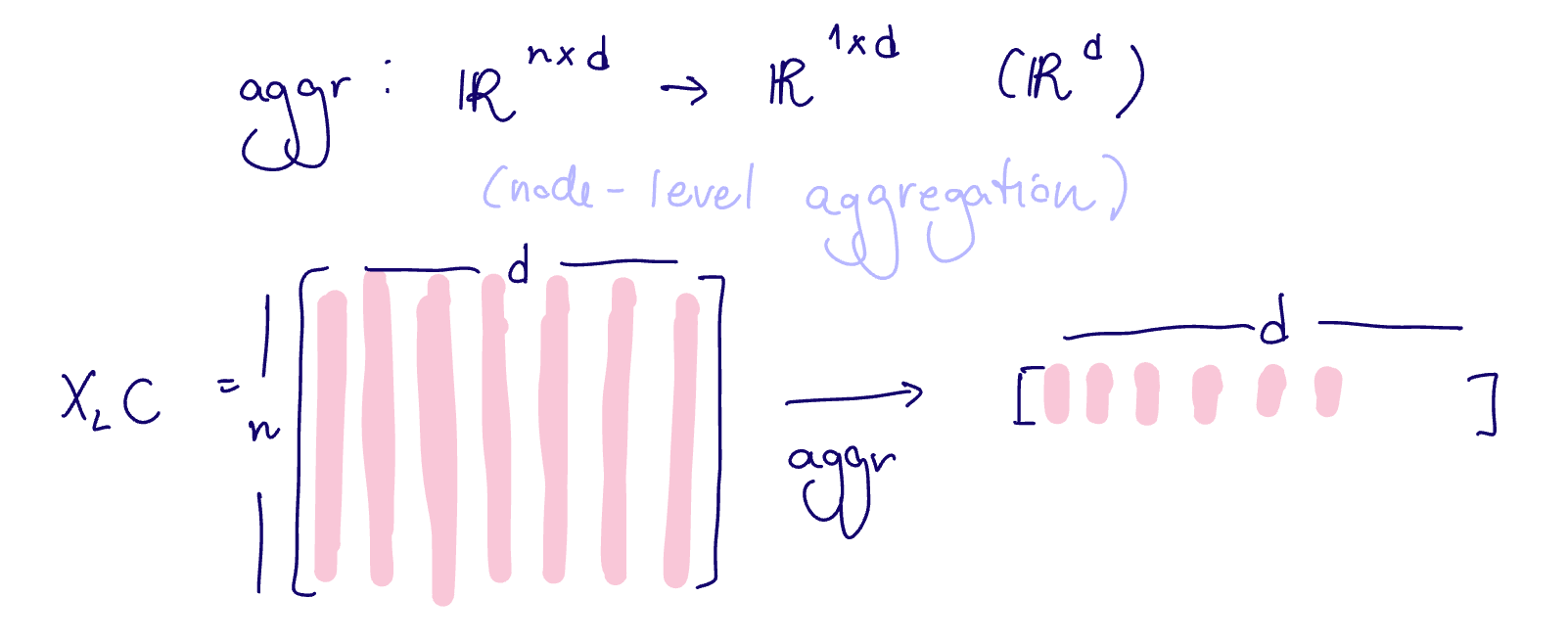
Typical aggregation functions are the mean, sum, max, min, median, etc

• this is now independent of $n$ (my aggregation functions don't change based on the size of my graph)
• permutation invariant since the aggregation functions are also permutation invariant
• this remains transferrable across graphs, unlike the fully connected readout layer

Let $G$ and $G^{\prime }$ be two graphs. A graph isomorphism between $G$ and $G^{\prime }$ is a bijection $M:V(G)\to V(G^{\prime })$ such that for all $i,j\in V(G)$

(see graph isomorphism)

Can we train a GNN to detect if graphs are isomorphic?

• ie, to produce identical outputs for graphs in the same equivalence class/graphs which are isomorphic, and different outputs for graphs that are not isomorphic?

Consider two graphs $G$ and $G^{\prime }$ without node features, with laplacian $L=V\mathrm{\Lambda }{V}^T$ and $L^{\prime }=V^{\prime }{\mathrm{\Lambda }}^{\prime }{V}^{\prime T}$. Further suppose that there is some ${\lambda }_j$ such that ${\lambda }_j\ne {\lambda }_i^{\prime }$ for all $i$ - ie, $L$ has at least one eigenvalue that is different from $L^{\prime }$.

Then there exists a graph convolution we can use to verify whether two graphs are NOT isomorphic, ie to test that $G\ne G^{\prime }$

Consider the following single-layer (linear) GNN

Define the graph feature $x$ to be white, ie such that $\mathbb{E}[{\hat{x}}_i]=1\mathrm{\forall }i=1,\dots ,n$.

Set $h_k=\{\begin{array}{l}1\text{ if }k=1\\ 0\text{otherwise}\end{array}$

Then we have

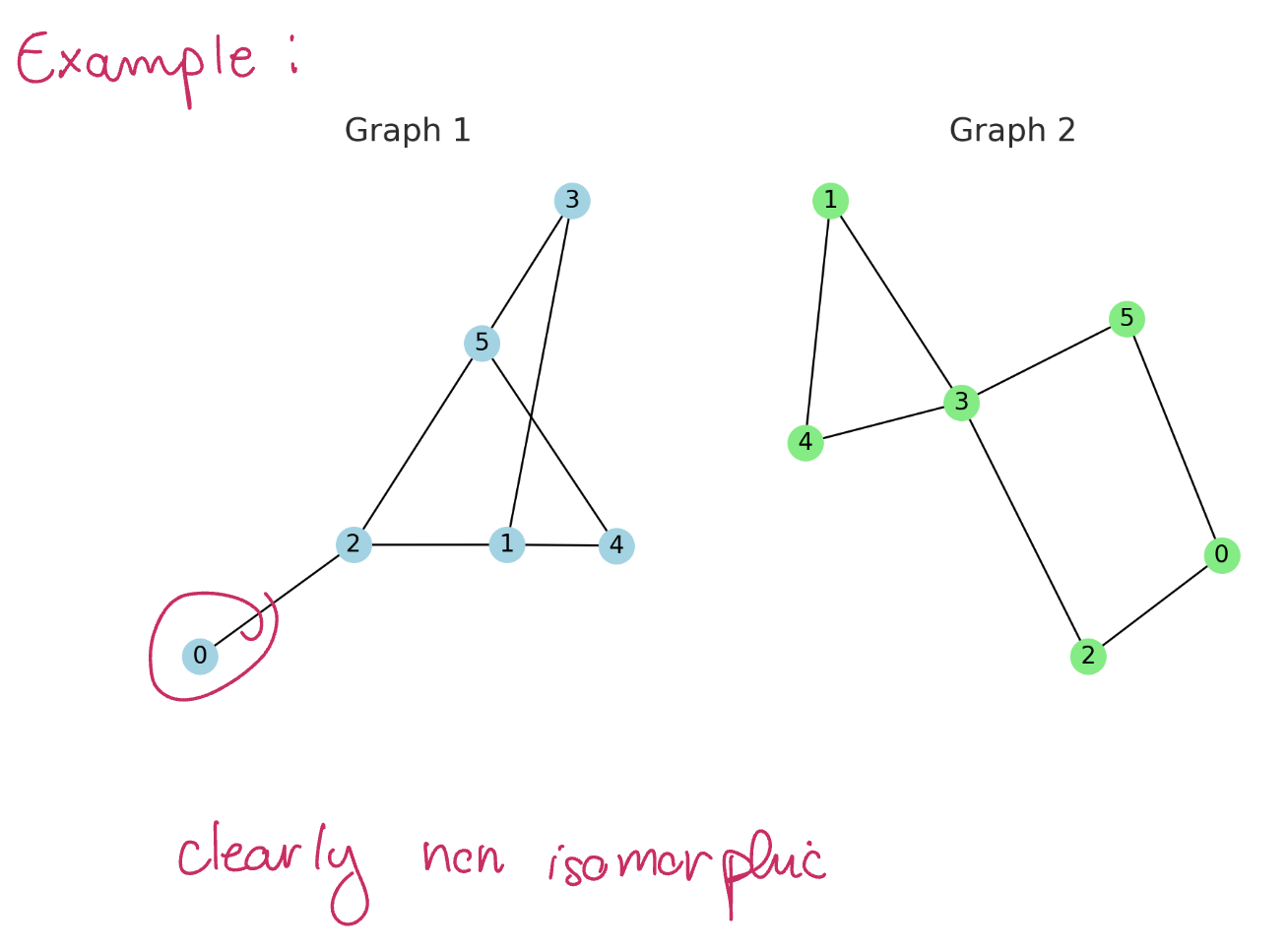
These graphs are clearly non-isomorphic, but their laplacian eigenvalues are the same!

Thus, a strong alternative is the

The Weisfeiler-Leman graph isomorphism test consists of running the color refinement algorithm for two graphs.

The color refinement algorithm is an algorithm to assign colorings to nodes.

Here, $f$ is a hash function that assigns colors.