stability-discriminability tradeoff for Lipschitz filters

Discriminability for lipschitz graph filters is the same at all frequencies. This means there is a tradeoff on benefits between having a large vs a small Lipschitz constant.

• with a small $c$, there is better stability for small perturbations on the eigenvalues
• However, if there are large perturbations on the graph, it is good to be more discriminative to notice these changes.

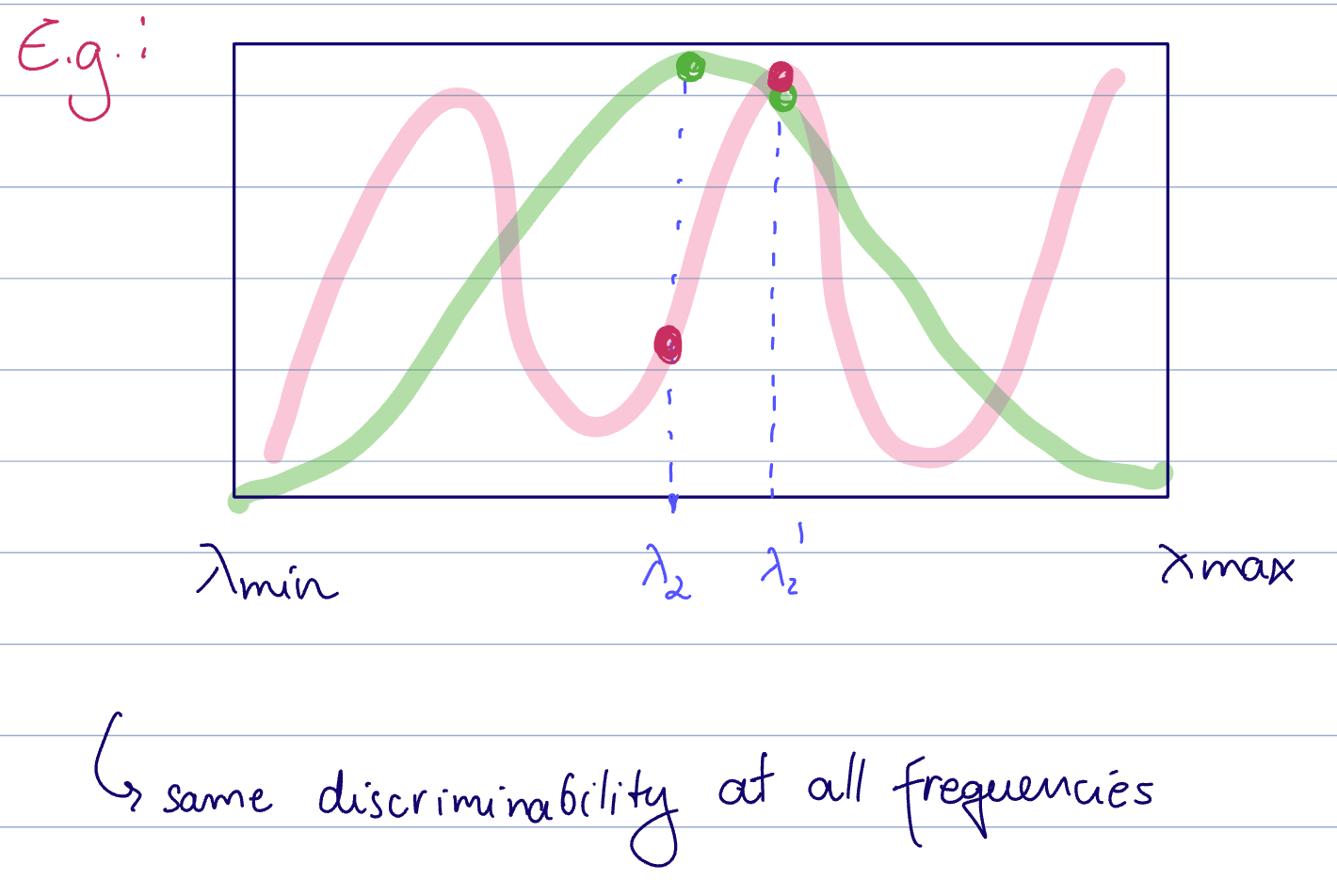
Here, green has a smaller $c$ and pink has a larger $c$.

${\lambda }_2^{\prime }$ is a perturbation on the second eigenvalue ${\lambda }_2$.

• The green filter is stable and gives a response that is very close to at both ${\lambda }_2$ and ${\lambda }_2^{\prime }$
• whereas the pink filter has a larger difference at the two sampled locations, but has better discriminability

Having a larger Lipschitz constant results in better discrimination between the responses, but less stability.