node-level task

subject:: Data Science Methods for Large Scale Graphs
parent:: Graph Signals and Graph Signal Processing
theme:: math notes

Consider the contextual SBM: $G=(V,E)$ undirected and $y\in \{-1,1{\}}^n$ (say $y_i$ represents the community of node $i$). The edges are random: $P(A_{ij})=P((i,j)\in E)=\{\begin{array}{l}\frac{a}{n},y_i=y_j\\ \frac{b}{n},\text{otherwise}\end{array}$ with node features/covariates
$x_i=\sqrt{\frac{u}{n}}{y}_{i}u+z_i$ where $u\sim N(0,1),z\sim N(0,I_n)$

If $u=1$ then $x_i\sim N(0,\sqrt{\frac{1}{n}(1{)}^2+1})$ and if $u=0$ then $x_i\sim N(0,\sqrt{\frac{1}{n}(-1{)}^2+1})$

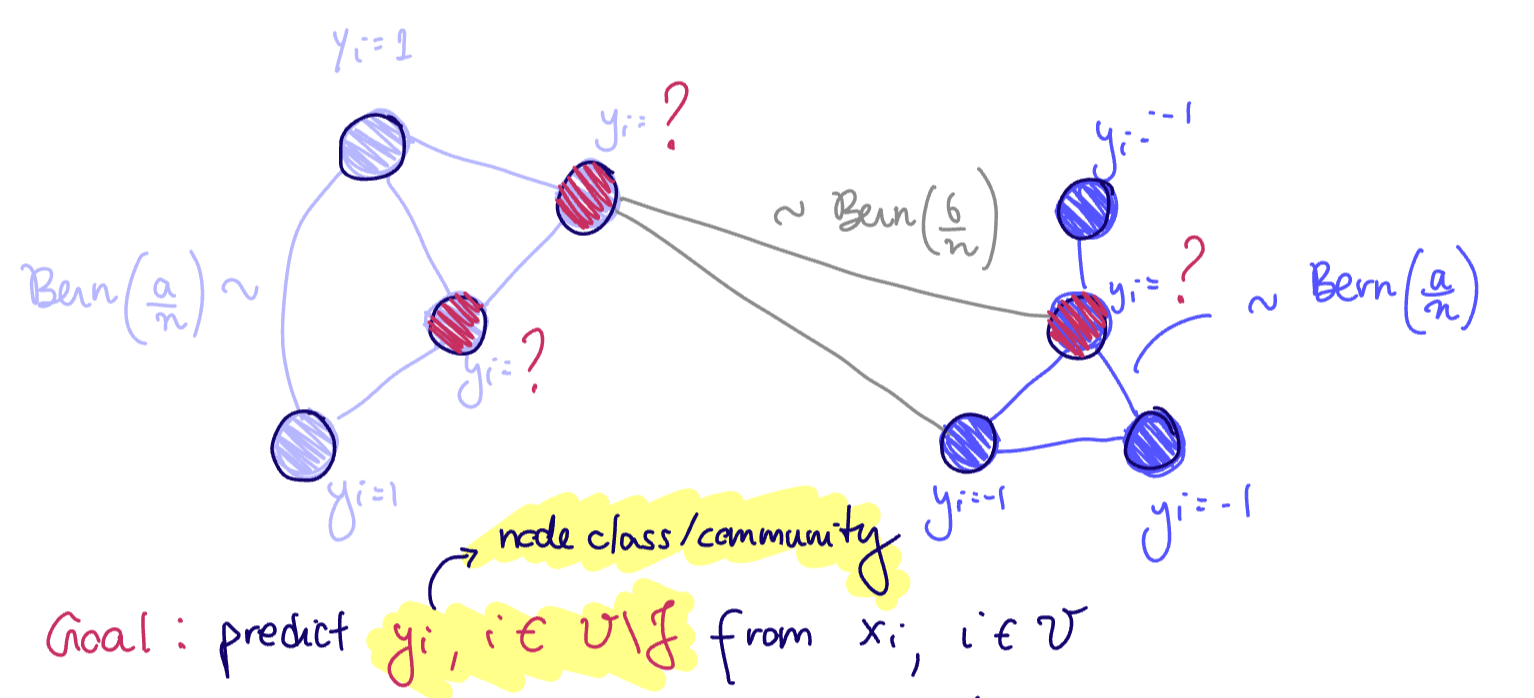
Goal: predict $y_i,i\in V\setminus J$ from $x_i\in V$
hypothesis class: the graph convolutions $\mathcal{F}\mathcal{=}$$\{z=\sum _{k=0}^{K+1}{h}_k{S}^{k}x,h_k\in \mathbb{R}\}$

Problem: Define a mask $M_f\in \{0,1{\}}^{|J|\times n}$. Then $M_f{\mathbb{1}}_n={\mathbb{1}}_{|J|}$ and ${\mathbb{1}}_{|J|}^T{M}_f={\mathbb{1}}_n^T$. Then we minimize:

Application: infer node's class/community/identity locally ie without needing communication, determining clustering techniques, which require eigenvectors (global graph information)