lipschitz graph convolutions of graph signals converge to lipschitz graphon filters
[[concept]]
Let
Let
Where
and are the graph and graphon convolution outputs respectively.
We want to show the outputs on the graph convolutions converge in the "induced graphon signal" sense to the outputs of the graphon convolution
- ie, want to show
where is the induced graphon signal for .
WLOG, we assume that
Define an partitioning index set
Where we fix some
Then, by the triangle inequality, we have
And we can bound
It is very easy to bound
For
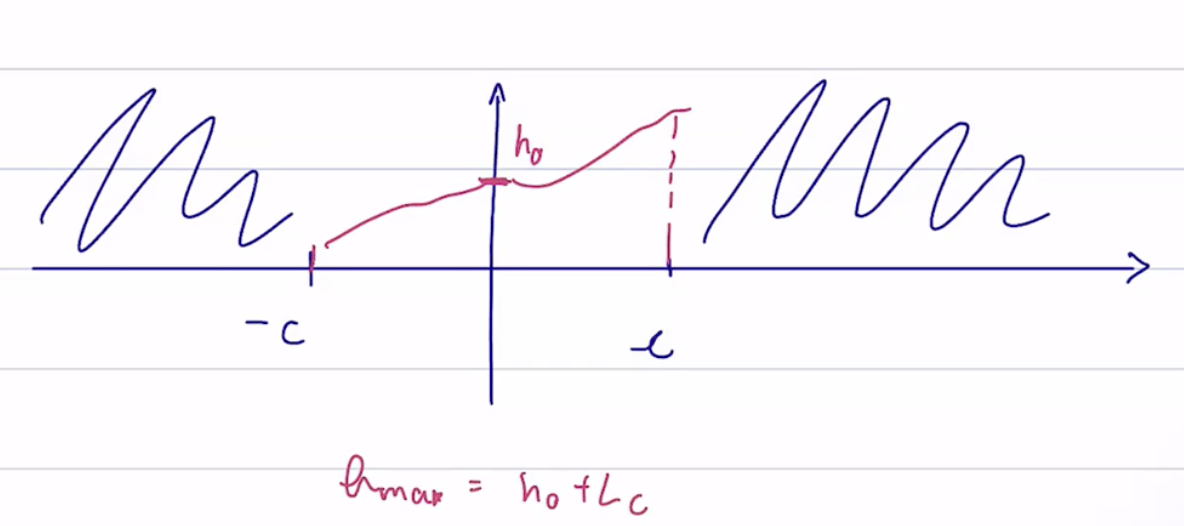
We don't care about the spectral intervals
Then we can write
We can see
Now, we need to bound
Note that we can write
We can do this because the
For
Where
Finally, for
Thus we get that
for all
It was difficult to show convergence for the GFT for spectral components associated with eigenvalues close to
Here, the same thing happens because graphon shift operator eigenvalues
accumulate at 0. The Lipschitz continuity addresses this by ensuring all spectral components near 0 are amplified in an increasingly "similar" way. We can see this by looking at how we defined
- If we fix
, in order to have , we need progressively smaller Lipschitz constant . ie, we need flatter and flatter functions - If we want
to get smaller (ie, we want the region where the spectral components cannot be discriminated to get smaller), we need a larger .
Review
{lipschitz graph convolutions} of graph signals converge to {lipschitz graphon filters}
For the convergence of Lipschitz graph convolutions to Lipschitz graphon convolutions, we define
Where
- If we fix
, in order to have , we need {ah||progressively smaller Lipschitz constant }. ie, we need {ah||flatter and flatter functions} - If we want
to get smaller (ie, we want {ha||a smaller indiscriminable region}), we need {==ha||a larger (more variation in the function) ==}
Mentions
| File | Last Modified |
|---|---|
| 2025-04-07 lecture 18 | 2025-10-02 |
| lipschitz graph convolutions of graph signals converge to lipschitz graphon filters | 2025-10-02 |
const { dateTime } = await cJS()
return function View() {
const file = dc.useCurrentFile();
return <p class="dv-modified">Created {dateTime.getCreated(file)} ֍ Last Modified {dateTime.getLastMod(file)}</p>
}